Question

Find the two geometric means between 20 and 5. 7. Solve: 44-32-3 8. Develop the identity for sin 2.4 using the identity for sin(A+ B).

Answer 1

Answer with explanation:

1.

Let a, and b be two numbers between 20 and 5 , which is in geometric progression.

So,the series is as Follows =20 , a, b, 5

Common ratio

`=\frac{\text{Second term}}{\text{First term}}`

`(20)/(a)=(a)/(b)=(b)/(5)\\\\b^2=5 a---(1)\\\\a^2=20 b\\\\(b^4)/(25)=20 b-----\text{Using 1}\\\\b^3=500\\\\b=(500)^{(1)/(3)}\\\\b=5* (4)^{(1)/(3)}\\\\5a=25* (4)^{(2)/(3)}\\\\a=5* (4)^{(2)/(3)}`

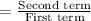
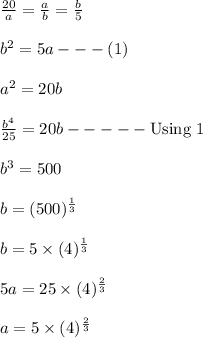
2.

44 -32-3

=12-3

=9

3.

⇒Sin (2.4)=Sin(2+0.4)

⇒Sin 2 ×Cos (0.4)+Cos 2 × Sin (0.4)

⇒Sin (A+B)=Sin A×Cos B+Cos A×Sin B