Question

You want to buy a $232,000 home. You plan to pay 20% as a down payment, and take out a 3.6% APR loan for the rest. a) How much is the loan amount going to be? b) What will your monthly payments be if the length of the loan is 10 years? c) What will your monthly payments be if the length of the loan is 20 years? d) Over the course of the entire loan, how much more do you end up paying with the longer loan? (Hint: take the difference of the total amounts paid)

Answer 1

The price of the home = 232,000

20% is down payment.

Part A:

`0.20*232000=46400`

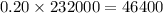
So, the loan amount will be =
`232000-46400=185600`

Loan amount or p = $185,600

Part B:

p = 185600

r =
`3.6/12/100=0.003`

n =
`10*12=120`

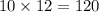
The EMI formula is :

`(p* r*(1+r)^(n) )/((1+r)^(n)-1 )`

Now putting the values in formula we get

`(185600* 0.003*(1+0.003)^(120) )/((1+0.003)^(120)-1 )`

=>
`(185600* 0.003*(1.003)^(120) )/((1.003)^(120)-1 )`

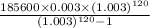
Monthly payments = $1844.02

Part C:

p = 185600

r =
`3.6/12/100=0.003`

n =
`20*12=240`

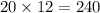
Now putting the values in formula we get

`(185600* 0.003*(1+0.003)^(240) )/((1+0.003)^(240)-1 )`

=>
`(185600* 0.003*(1.003)^(240) )/((1.003)^(240)-1 )`

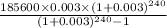
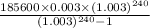
Monthly payments = $1085.96

Part D:

For 10 year loan you have to pay =
`120*1844.02=221282.40`

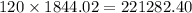
For 20 years loan you have to pay =
`240*1085.96=260630.40`

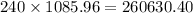
So, you ended up paying
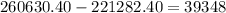`260630.40-221282.40=39348` dollars more in longer loan.

The difference is $39,348.