Answer:
Given,
The initial population ( on 2010 ) = 40,000,
Let r be the rate of increasing population per year,
Thus, the function that shows the population after t years,
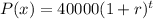
And, the population after 5 years ( on 2015 ) is,
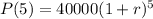
According to the question,
P(5) = 50,000,



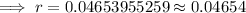
So, the population is increasing the with rate of 0.04654,
And, the population after t years would be,
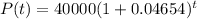
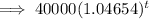
Since, the exponential function is,
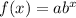
Hence, by comparing,
a = 40000,
b = 1.04654