Question

Use induction to prove: For every integer n > 1, the number n5 - n is a multiple of 5.

Answer 1

we need to prove : for every integer n>1, the number
`n^(5)-n` is a multiple of 5.

1) check divisibility for n=1,
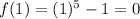`f(1)=(1)^(5)-1=0` (divisible)

2) Assume that
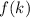`f(k)` is divisible by 5,
`f(k)=(k)^(5)-k`

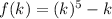
3) Induction,

`f(k+1)=(k+1)^(5)-(k+1)`

`=(k^(5)+5k^(4)+10k^(3)+10k^(2)+5k+1)-k-1`

`=k^(5)+5k^(4)+10k^(3)+10k^(2)+4k`

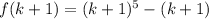
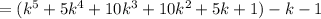
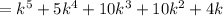
Now,
`f(k+1)-f(k)`

`f(k+1)-f(k)=k^(5)+5k^(4)+10k^(3)+10k^(2)+4k-(k^(5)-k)`

`f(k+1)-f(k)=k^(5)+5k^(4)+10k^(3)+10k^(2)+4k-k^(5)+k`

`f(k+1)-f(k)=5k^(4)+10k^(3)+10k^(2)+5k`

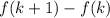
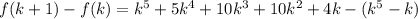
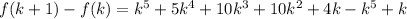
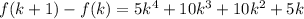
Take out the common factor,

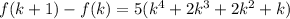`f(k+1)-f(k)=5(k^(4)+2k^(3)+2k^(2)+k)` (divisible by 5)

add both the sides by f(k)

`f(k+1)=f(k)+5(k^(4)+2k^(3)+2k^(2)+k)`

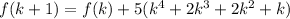
We have proved that difference between
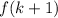`f(k+1)` and
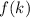`f(k)` is divisible by 5.

so, our assumption in step 2 is correct.

Since
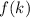`f(k)` is divisible by 5, then
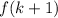`f(k+1)` must be divisible by 5 since we are taking the sum of 2 terms that are divisible by 5.

Therefore, for every integer n>1, the number
`n^(5)-n` is a multiple of 5.