Question

3. Given the differential equation y"+y= 0 and the set of two functions sint-cost, sint + cost, show that this a fundamental set of functions for the equation, and note the interval(s) over which this is true. wken (osxsihx | Cos sint

Answer 1

Answer with explanation:

Given the differential equation

y''+y=0

The two function let

`y_1= sint -cost`

`y_2=sint+ cost`

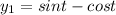
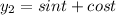
Differentiate
`y_1 and y_2`

Then we get

`y'_1= cost+sint`

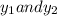
`y'_2=cost-sint`

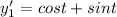
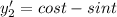
Because
`\frac{\mathrm{d} sinx}{\mathrm{d} x} = cosx`

`\frac{\mathrm{d}cosx }{\mathrm{d}x}= -sinx`

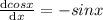
We find wronskin to prove that the function is independent/ fundamental function.

w(x)=
`\begin{vmatrix} y_1&y_2\\y'_1&y'_2\end{vmatrix}`

`w(x)=\begin{vmatrix}sint-cost&sint+cost\\cost+sint&cost-sint\end{vmatrix}`

`w(x)=(sint-cost)(cost-sint)- (sint+cost)(cost+sint)`

`w(x)=sintcost-sin^2t-cos^2t+sintcost-sintcost-sin^2t-cos^2t-sintcost`

`w(x)=-sin^2t-cos^2t`

`sin^2t+cos^2t=1`

`w(x)=-2\\eq0`

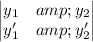
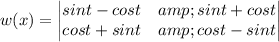
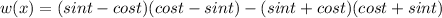
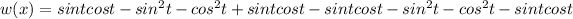
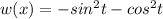
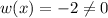
Hence, the given two function are fundamental set of function on R.