Question

Which transformation from the graph of a function f(x) describes the graph of f(x)-1?

Answer 1

Explanation:

Any side to side movement of a function will be reflected inside a set of parenthesis with the x. For example, if the function was a parabola, the parent graph could be, very simply,

`y=x^2`

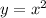
Side to side movement would make the equation look like this:

`y=(x-h)^2`

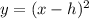
where h is the x coordinate of the vertex.

Up or down movment would make the equation look like this:

`y=x^2+k` for movement upwards, or

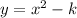`y=x^2-k` for movement downwards. The k represents the y coordiante of the vertex in this parabola.

Because our function has NO numbers inside the parenthesis with the f(x), but it has a -1 after, we are moving the parent graph of this function, whatever it is, down one from its starting position.