Question

If records indicate that 15 houses out of 1000 are expected to be damaged by fire in any year, what is the probability that a woman who owns 14 houses will have fire damage in 2 of them in a year? (Round your answer to five decimal places.)

Answer 1

Answer: 0.01708

Explanation:

Given : If records indicate that 15 houses out of 1000 are expected to be damaged by fire in any year.

i.e. the probability that house damaged buy fire in a year :
`p=(15)/(1000)=0.015`

The formula for binomial distribution is given by :-

`^(n)C_xp^x(1-p)^(n-x)`

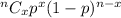
Now, the probability that a woman who owns 14 houses will have fire damage in 2 of them in a year (put n=14 and x=2), we get

`^(14)C_2(0.015)^2(1-0.015)^(14-2)\\\\=(14!)/(2!(14-2)!)(0.015)^2(0.985)^(12)\\\\=0.0170788520518\approx0.01708`

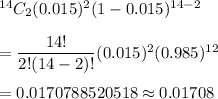
Hence, the required probability = 0.01708