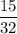Question

Julie has 5 cherry lollipops,1 lime lollipops, and 2 grape lollipops in a bag. She is going to select one lollipop, replace the lollipop in the bag, and then select a second one. What is the probability that Julie will select a cherry lollipop and then a lollipop other than grape?

a.)6/8

b.)11/16

c.)15/32

d.)10/64

Answer 1

Answer:
`(15)/(32)`

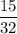
Explanation:

Given : The number of cherry lollipop = 5

The total number of lollipop = 8

the number of lollipops other than grape =6

The probability of selecting a cherry lollipop is given by :_

`\text{P(Cherry)}=(5)/(8)`

The probability of selecting a lollipop other than grape is given by :_

`\text{P(Other than grape)}=(6)/(8)`

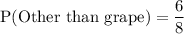
Since, there is replacement , then the events are independent of each other.

Now, the probability that Julie will select a cherry lollipop and then a lollipop other than grape is given by :-

`\text{P(Cherry and other than grape)}=(5)/(8)*(6)/(8)=(15)/(32)`

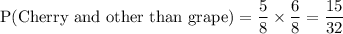
Hence, the required probability =
`(15)/(32)`