Question

In a survey, 22 people were asked how much they spent on their child's last birthday gift. The results were roughly bell-shaped with a mean of $32 and standard deviation of $17. Construct a confidence interval at a 98% confidence level.

Answer 1

`19.22\:<\:\mu\:<\:44.78`

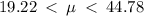
Explanation:

Tthe population is normally distributed and the sample size is
`n=22\:<\:30`.

Since the population standard deviation
`\sigma` is unknown and the sample standard deviation
`s`, must replace it, the t distribution must be used for the confidence interval.

Hence with degrees of freedom of 21,
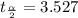`t_{(\alpha)/(2) }=3.527`.(Read from the t distribution table)

The 98% confidence interval can be constructed using the formula:

`\bar X-t_{(\alpha)/(2)}((s)/(√(n) ) )\:<\:\mu\:<\:\bar X+t_{(\alpha)/(2)}((s)/(√(n) ) )`.

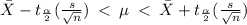From the question the sample mean is
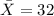`\bar X=32`dollars and the sample standard deviation is
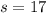`s=17` dollars.

We substitute the values into the formula to get

`32-3.527((17)/(√(22) ) )\:<\:\mu \:<\:32+3.527((17)/(√(22) ) )`

`19.22\:<\:\mu\:<\:44.78`

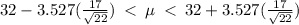
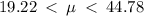
Therefore, we can be 98% confident that the population mean is between is between 19.22 and 44.78 dollars.