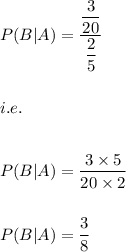Answer:
The probability of drawing a second green marble, given that the first marble is green is:

Explanation:
Let A denote the event that first marble is green.
B denote the event that the second marble is green.
A∩B denote the event that both the marbles are green.
Let P denote the probability of an event.
We are asked to find:
P(B|A) i.e. probability of drawing a second green marble, given that the first marble is green.
We know that:
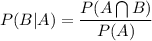
Probability of drawing one green marble is 2/5 i.e.
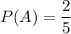
The probability of drawing two green marbles from the urn without replacement is 3/20 i.e.
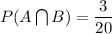
Hence, we have: