Question

Given the system of linear equations. Choose all of the options that could be used to solve the system using addition

{x+y=7
12x+y = 5
Multiply the first equation by -1 and add the equations together.
Multiply the second equation by-1 and the first equation by -1, then add the equations together.
Multiply the second equation by-1 and add the equations together.
Multiply the first equation by-2 and add the equations together.
Multiply the first equation by 2 and the second equation by -1, then add the equations together.

Answer 1

Hello!

The answer is:

The only operations that could be used to solve the system using addition are the first and the third operation.

Why?

To solve the problem, we need to check and discard each of the given option to see if the operations works to solve the system using addition, so, trying the given options.

The system of equation is:

`x+y=7\\12x+y=5`

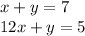
We can see that the only way to solve the system using addition, is multiplying the first or the second equation by -1, so, we can eliminate the variable "y", let's prove that:

- First operation: Multiplying the first equation by -1 and add the equations together,

`x+y=7\\12x+y=5`

`x*(-1)+y*(-1)=7*(-1)\\12x+y=5`

`-x+-y=-7\\12x+y=5`

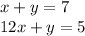
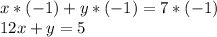
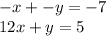
Adding the equations, we have:

`12x-x+y-y=5-7`

`11x+=5-7`

`11x+=-2`

`x=-(2)/(11)`

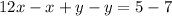
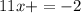
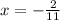
We can see that we can solve the problem using the first operation the operation.

- Third operation: Multiplying the second equation by -1 and add the equations together,

`x+y=7\\12x+y=5`

`x+y=7\\12x*(-1)+y*(-1)=5*(-1)`

`x+y=7\\-12x+-y=-5`

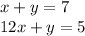
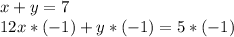
Adding the equations we have:

`-12x+x+y-y=-5+7`

`-11x=2`

`x=-(2)/(11)`

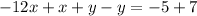
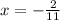
We can see that we can solve the problem using the third operation.

Also, we can see that in both equations the variable "y" has the same coefficient, the only operations that could work to solve the system using addition are the first and the third operation.

Have a nice day!