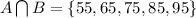Answer:
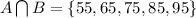
Explanation:
Set A contains odd numbers between 0 and 100.
So, the elements in set A are as, Set A
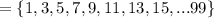
Set B contains the numbers between 50 and 150, that are evenly divisible by 5.
So, the elements in set B are are as, Set B
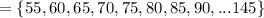
Now, we need to find
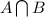
To find
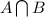 , we need to find the common elements in Set A and Set B.
, we need to find the common elements in Set A and Set B.
The common elements in Set A and Set B is
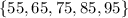
So,