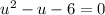Question

Which quadratic equation is equivalent to (X-4)^2-(x-4)-6=0
Where u=x-4?

Answer 1

see explanation

Explanation:

letting u = x - 4 means the equation can now be expressed as a quadratic

u² - u - 6 = 0 ← quadratic equation in u

Answer 2

`u^2 - u - 6 = 0`

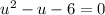
Explanation:

We are given
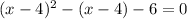`(x - 4)^2 - (x -4) -6 = 0` and u = x - 4

Now we have to replace (X - 4) by "u".

So, we get

`u^2 - u - 6 = 0`

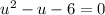
Here the highest degrees of the equation is 2. Which is called a quadratic equation.

The general form of quadratic equation is
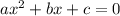`ax^2 + bx + c = 0`, where a≠ 0.

Therefore, the answer is
`u^2 - u - 6 = 0`