Answer:
Part 1: The polygon ABCDE reflected across y-axis to get the polygon MNOPQ. So, the polygon ABCDE congruent to polygon MNOPQ.
Part 2: The vertices of polygon VWXYZ are V(1, 3), W(-1, 7), X(-7, 7), Y(-5, 3), and Z(-3, 1).
Explanation:
Part 1:
The vertices of the polygon ABCDE are A(2, 8), B(4, 12), C(10, 12), D(8, 8), and E(6, 6).
The vertices of the polygon MNOPQ are M(-2, 8), N(-4, 12), O(-10, 12), P(-8, 8), and Q(-6, 6).
We need to find the transformation or sequence of transformations that can be performed on polygon ABCDE to show that it is congruent to polygon MNOPQ.
The relation between the vertices of ABCDE and MNOPQ are defined as
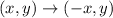
It means the polygon ABCDE reflected across y-axis to get the polygon MNOPQ. So, the polygon ABCDE congruent to polygon MNOPQ.
Part 2:
If polygon MNOPQ is translated 3 units right and 5 units down, then
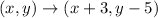
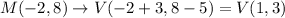

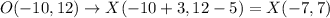
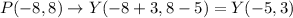
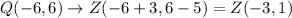
Therefore the vertices of polygon VWXYZ are V(1, 3), W(-1, 7), X(-7, 7), Y(-5, 3), and Z(-3, 1).