Hello!
The answer is:
The ordered pair satisfies the following system of equations since it satisfies both equations.
Why?
If we need to know if the ordered pair (-11/3,2/3) satisfies the system of equations we need to evaluate it and check if it satisfies both equations, we must remember that the condition that determines if the system of equations is satisfied is that both equations must be satisfied.
So, evaluating the ordered pair, we have:
First equation:
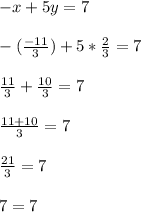
We have that the equation is satisfied.
Second equation:

We have that the equation is satisfied.
Hence, we have that the ordered pair satisfies the system of equations since it satisfies both equations
Have a nice day!