Question

Please help me! This is is rational function and I don’t know how to/ don’t remember how do this! How would I find and write the equation for it?

Answer 1

An answer is

`\displaystyle f\left(x\right)=(\left(x+1\right)^3)/(\left(x+2\right)^2\left(x-1\right))`

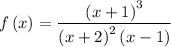
Step-by-step explanation:

Template:

`\displaystyle f(x) = a \cdot ((\cdots) \cdots (\cdots))/(( \cdots )\cdots( \cdots ))`

There is a nonzero horizontal asymptote which is the line y = 1. This means two things: (1) the numerator and degree of the rational function have the same degree, and (2) the ratio of the leading coefficients for the numerator and denominator is 1.

The only x-intercept is at x = -1, and around that x-intercept it looks like a cubic graph, a transformed graph of
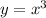`y = x^3`; that is, the zero looks like it has a multiplicty of 3. So we should probably put
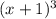`(x+1)^3` in the numerator.

We want the constant to be a = 1 because the ratio of the leading coefficients for the numerator and denominator is 1. If a was different than 1, then the horizontal asymptote would not be y = 1.

So right now, the function should look something like

`\displaystyle f(x) = ((x+1)^3)/(( \cdots )\cdots( \cdots )).`

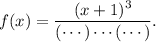
Observe that there are vertical asymptotes at x = -2 and x = 1. So we need the factors
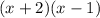`(x+2)(x-1)` in the denominator. But clearly those two alone is just a degree-2 polynomial.

We want the numerator and denominator to have the same degree. Our numerator already has degree 3; we would therefore want to put an exponent of 2 on one of those factors so that the degree of the denominator is also 3.

A look at how the function behaves near the vertical asympotes gives us a clue.

Observe for x = -2,

• as x approaches x = -2 from the left, the function rises up in the positive y-direction, and
• as x approaches x = -2 from the right, the function rises up.

Observe for x = 1,

• as x approaches x = 1 from the left, the function goes down into the negative y-direction, and
• as x approaches x = 1 from the right, the function rises up into the positive y-direction.

We should probably put the exponent of 2 on the
`(x+2)` factor. This should help preserve the function's sign to the left and right of x = -2 since squaring any real number always results in a positive result.

So now the function looks something like

`\displaystyle f(x) = ((x+1)^3)/((x+2 )^2(x-1)).`

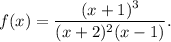
If you look at the graph, we see that
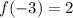`f(-3) = 2`. Sure enough

`\displaystyle f(-3) = ((-3+1)^3)/((-3+2 )^2(-3-1)) = (-8)/((1)(-4)) = 2.`

And checking the y-intercept, f(0),

`\displaystyle f(0) = ((0+1)^3)/((0+2 )^2(0-1)) = (1)/(4(-1)) = -1/4 = -0.25.`

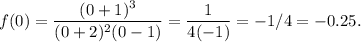
and checking one more point, f(2),

`\displaystyle f(2) = ((2+1)^3)/((2+2 )^2(2-1)) = (27)/((16)(1)) \approx 1.7`

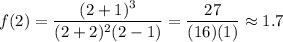
So this function does seem to match up with the graph. You could try more test points to verify.

======

If you're extra paranoid, you can test the general sign of the graph. That is, evaluate f at one point inside each of the key intervals; it should match up with where the graph is. The intervals are divided up by the factors:

• x < -2. Pick a point in here and see if the value is positive, because the graph shows f is positive for all x in this interval. We've already tested this: f(-3) = 2 is positive.
• -2 < x < -1. Pick a point in here and see if the value is positive, because the graph shows f is positive for all x in this interval.
• -1 < x < 1. Pick a point here and see if the value is negative, because the graph shows f is negative for all x in this interval. Already tested since f(0) = -0.25 is negative.
• x > 1. See if f is positive in this interval. Already tested since f(2) = 27/16 is positive.

So we need to see if -2 < x < -1 matches up with the graph. We can pick -1.5 as the test point, then

`\displaystyle f(-1.5) = (\left(-1.5+1\right)^3)/(\left(-1.5+2\right)^2\left(-1.5-1\right)) = ((-0.5)^3)/((0.5)^2(-2.5)) \\= (-0.5)^3 \cdot (1)/((0.5)^2) \cdot (1)/(-2.5)`

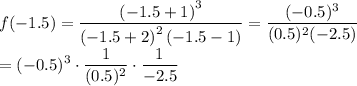
We don't care about the exact value, just the sign of the result.

Since
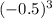`(-0.5)^3` is negative,
`(0.5)^2` is positive, and
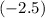`(-2.5)` is negative, we really have a negative times a positive times a negative. Doing the first two multiplications first, (-) * (+) = (-) so we are left with a negative times a negative, which is positive. Therefore, f(-1.5) is positive.