Question

In a batch of​ 8,000 clock radios 7​% are defective. A sample of 1313 clock radios is randomly selected without replacement from the​ 8,000 and tested. The entire batch will be rejected if at least one of those tested is defective. What is the probability that the entire batch will be​ rejected

Answer 1

Answer: Probability that the entire batch will be rejected is 0.611.

Explanation:

Since we have given that

Number of clock radios in a batch = 8000

Probability of defective clock radio = 7%

According to question, we have mentioned that A sample of 13 clock radios is randomly selected without replacement from the​ 8,000 and tested.

We will use "Binomial distribution":

here, n = 13 and

p (probability of success) = 7% = 0.07

so, we need to find that

P(the entire batch will be rejected) = P(at least one of those test is defected)

So, it becomes,

P(at least one of those tested is defective) = 1 - P(none are defective)

So, P(none are defective ) is given by

`(1-0.07)^(13)\\\\=0.93^(13)\\\\=0.389`

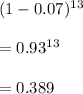
So, P(at least one of those tested is defective) = 1 - P(none are defective)

= 1 - 0.389

= 0.611

Hence, Probability that the entire batch will be rejected is 0.611.