Question

A 0.144 kg baseball moving 28.0 m/s strikes a stationary 5.25 kg brick resting on small rollers so it moves without significant friction. After hitting the brick, the baseball bounces back, and the brick moves forward at 1.1 m/s (a) For determining baseball's speed after the collision, do you need to use momentum conservation, energy conservation or both? Give reasons for your answer (Marks will only be awarded if reasoning is qiven). (b) What is the baseball's speed after the collision? (c) Find the total mechanical energy before and after the collision. (d) Show that the collision is inelastic. (e) Is the kinetic energy of the system conserved? Give a reason. (f Is the total energy of the system conserved? Give a reason

Answer 1

(a) Only momentum conservation

In order to find the speed of the ball, momentum conservation is enough. In fact, we have the following equation:

`m u + M U = m v + M V`

where

m is the mass of the baseball

u is the initial velocity of the baseball

M is the mass of the brick

U is the initial velocity of the brick

v is the final velocity of the baseball

V is the final velocity of the brick

In this problem we already know the value of: m, u, M, U, and V. Therefore, there is only one unknown value, v: so this equation is enough to find its value.

(b) 12.1 m/s

Using the equation of conservation of momentum written in the previous part:

`m u + M U = m v + M V`

where we have:

m = 0.144 kg

u = +28.0 m/s (forward)

M = 5.25 kg

U = 0

V = +1.1 m/s (forward)

We can solve the equation to find v, the velocity of the ball:

`v=(mu-MV)/(m)=((0.144 kg)(+28.0 m/s)-(5.25 kg)(+1.1 m/s))/(0.144 kg)=-12.1 m/s`

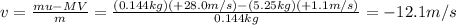
And the sign indicates that the ball bounces backward, so the speed is 12.1 m/s.

(c) 56.4 J, 13.7 J

The total mechanical energy before the collision is just equal to the kinetic energy of the baseball, since the brick is at rest; so:

`E_i = (1)/(2)mu^2 = (1)/(2)(0.144 kg)(28.0 m/s)^2=56.4 J`

The total mechanical energy after the collision instead is equal to the sum of the kinetic energies of the ball and the brick after the collision:

`E_f = (1)/(2)mv^2 + (1)/(2)MV^2 = (1)/(2)(0.144 kg)(12.1 m/s)^2 + (1)/(2)(5.25 kg)(1.1 m/s)^2=13.7 J`

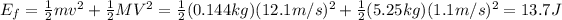
(d)

A collision is:

- elastic when the total mechanical energy is conserved before and after the collision

- inelastic when the total mechanical energy is NOT conserved before and after the collision

In this problem we have:

- Energy before the collision: 56.4 J

- Energy after the collision: 13.7 J

Since energy is not conserved, this is an inelastic collision.

(e) No

As shown in part (c) and (d), the kinetic energy of the system is not conserved. This is due to the fact that in inelastic collisions (such as this one), there are some internal/frictional forces that act on the system, and that cause the dissipation of part of the initial energy of the system. This energy is not destroyed (since energy cannot be created or destroyed), but it is simply converted into other forms of energy (mainly heat and sound).