Answer:
- Function:
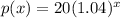
- Range: option D. 20 ≤ x ≤ 27.37
Step-by-step explanation:
The function must meet the rule that the pay starts at $20 and it increases each hour by 4%.
A table will help you to visualize the rule or pattern that defines the function:
x (# hours) pay ($) = p(x)
0 20 . . . . . . . . [starting pay]
1 20 × 1.04 . . . [ increase of 4%]
2 20 × 1.04² . . . [increase of 4% over the previous pay]
x 20 × 1.04ˣ
Hence, the function is:
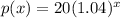
The range is the set of possible outputs of the function. To find the range, take into account that this is a growing exponential function, meaning that the least output is the starting point, and from there the output will incrase.
The choices name x this output. Hence, the starting point is x = 20 and the upper bound is when the number of hours is 8: 20(1.04)⁸ = 27.37.
Then the range is from 20 to 27.37 (dollars), which is represented by 20 ≤ x ≤ 27.37 (option D from the choices).