Question

Two bonds funds pay interest at rates of 3% Money invested for one year in the first fund earns $360 interest. The same amount invested in the other fund earns $480. find the lower rate of interest.

Answer 1

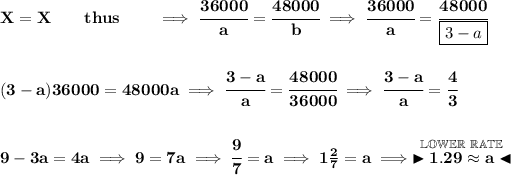
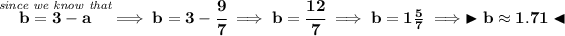a = interest rate for first bond.

b = interest rate for second bond.

we know the rates add up to 3%, so a + b = 3.

we also know that investing the same amount hmm say $X gives us the amounts of 360 and 480 respectively.

let's recall that to get a percentage of something we simply
`\bf \begin{array} \cline{1-1} \textit{a\% of b}\\ \cline{1-1} \\ \left( \cfrac{a}{100} \right)\cdot b \\\\ \cline{1-1} \end{array}`

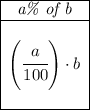
so then, "a percent" of X is just (a/100)X = 360.

and "b percent" of X is just (b/100)X = 480.

`\bf a+b=3\qquad \implies \qquad \boxed{b}=3-a~\hfill \begin{cases} \left( (a)/(100) \right)X=360\\\\ \left( (b)/(100) \right)X=480 \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \left( \cfrac{a}{100} \right)X=360\implies X=\cfrac{360}{~~(a)/(100)~~}\implies X=\cfrac{36000}{a} \\\\\\ \left( \cfrac{b}{100} \right)X=480\implies X=\cfrac{480}{~~(b)/(100)~~}\implies X=\cfrac{48000}{b} \\\\[-0.35em] ~\dotfill`

`\bf X=X\qquad thus\qquad \implies \cfrac{36000}{a}=\cfrac{48000}{b}\implies \cfrac{36000}{a}=\cfrac{48000}{\boxed{3-a}} \\\\\\ (3-a)36000=48000a\implies \cfrac{3-a}{a}=\cfrac{48000}{36000}\implies \cfrac{3-a}{a}=\cfrac{4}{3} \\\\\\ 9-3a=4a\implies 9=7a\implies \cfrac{9}{7}=a\implies 1(2)/(7)=a\implies \stackrel{\mathbb{LOWER~RATE}}{\blacktriangleright 1.29\approx a \blacktriangleleft}`

`\bf \stackrel{\textit{since we know that}}{b=3-a}\implies b=3-\cfrac{9}{7}\implies b=\cfrac{12}{7}\implies b=1(5)/(7)\implies \blacktriangleright b \approx 1.71 \blacktriangleleft`