Question

Problem #1. (a) Prove that if z is irrational, then underroot x is irrational.

Answer 1

Answer with explanation:

It is given that z is an irrational complex number.

Z= x + i y

Where x is real part and y is Imaginary part.x and y can be any Real number.

If z is an irrational complex number , then both real part and imaginary part should be a complex number.That is x, y ∈Q, then ,Q= Set of Irrationals.

It means , x and y both should be an irrational number.

So, if x is any irrational number then,
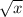`√(x)` will be also an irrational number.