Suppose
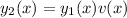 is another solution. Then
is another solution. Then

Substituting these derivatives into the ODE gives

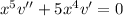
Let
 , so that
, so that

Then the ODE becomes
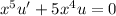
and we can condense the left hand side as a derivative of a product,
![(\mathrm d)/(\mathrm dx)[x^5u]=0](https://img.qammunity.org/2020/formulas/mathematics/college/ob8rrh553xgsx1w5umuxx7nqqnhoczkzsy.png)
Integrate both sides with respect to
 :
:
![\displaystyle\int(\mathrm d)/(\mathrm dx)[x^5u]\,\mathrm dx=C](https://img.qammunity.org/2020/formulas/mathematics/college/43qx6ba3um95u42dwz28vdqeqzb5igucz2.png)
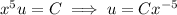
Solve for
 :
:
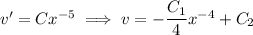
Solve for
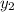 :
:
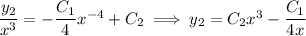
So another linearly independent solution is
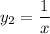 .
.