Answer:
The total number of ways are:
462
Explanation:
When we are asked to select r items from a set of n items that the rule that is used to solve the problem is:
Method of combination.
Here the total number of bills of different values are: 7
i.e. n=7
( $1, $2, $5, $10, $20, $50, and $100 )
and there are atleast five of each type of bill.
Also, we have to choose 5 bills i.e. r=5
The repetition is allowed while choosing bills.
Hence, the formula is given by:

Hence, we get:
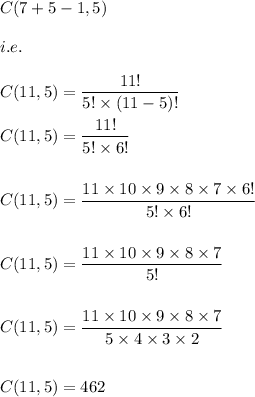
Hence, the answer is:
462