For this case we have that by definition, the slope of a line is given by:
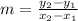
According to the data we have the following points:
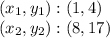
Substituting we have:
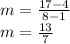
So, the slope is
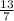
ANswer:
The student's mistake was to erroneously subtract the "x" coordinates from the points