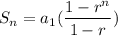Question

Which formula can be used to sum the first n terms of a geometric sequence?

Answer 1

The formula which can be used to find the sum of the first n terms of a geometric sequence is:

`S_n=a_1((1-r^n)/(1-r))`

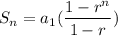
Explanation:

Geometric sequence--

A sequence is said to be a geometric sequence if each of the term of a sequence is a constant multiple of the preceding term of the sequence.

This constant multiple is known as a common ratio and is denoted by r.

Also, if the first term of the sequence is:
`a_1`

Then the sequence is given by:

`a_1,\ a_2=a_1r,\ a_3=a_1r^2,\ a_4=a_1r^3,\ .............a_n=a_1r^(n-1),\ .....`

The sum of the first n terms of the sequence is given by:

`S_n=a_1((1-r^n)/(1-r))`

Answer 2

The correct answer option is B.
`S _ n = a _ 1 [ \frac { 1 - r ^ n } { 1 - r } ]`.

Explanation:

The following is the formula that is used to find the sum of a geometric progession:

`S _ n = a _ 1 [ \frac { 1 - r ^ n } { 1 - r } ]`

where
`S_n` is the sum,
`a_1` is the first term,
`r` is the common ratio while
`n` is the number of terms.