Question

In a sample of 8 high school students, they spent an average of 28.8 hours each week doing sports with a sample standard deviation of 3.2 hours. Find the 95% confidence interval, assuming the times are normally distributed.

Answer 1

`26.12\:<\:\mu\:<\:31.48`

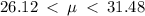
Explanation:

Since the population standard deviation
`\sigma` is unknown, and the sample standard deviation
`s`, must replace it, the
`t` distribution must be used for the confidence interval.

The sample size is n=8.

The degree of freedom is
`df=n-1`,
`\implies df=8-1=7`.

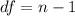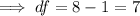With 95% confidence level, the
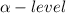`\alpha-level`(significance level) is 5%.

Hence with 7 degrees of freedom,
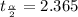`t_{(\alpha)/(2) }=2.365`. (Read from the t-distribution table see attachment)

The 95% confidence interval can be found by using the formula:

`\bar X-t_{(\alpha)/(2)}((s)/(√(n) ) )\:<\:\mu\:<\:\bar X+t_{(\alpha)/(2)}((s)/(√(n) ) )`.

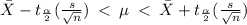The sample mean is
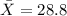`\bar X=28.8` hours.

The sample sample standard deviation is
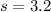`s=3.2` hours.

We now substitute all these values into the formula to obtain:

`28.8-2.365((3.2)/(√(8) ) )\:<\:\mu\:<\:28.8+2.365((3.2)/(√(8) ) )`.

`26.12\:<\:\mu\:<\:31.48`

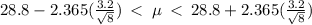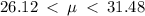
We are 95% confident that the population mean is between 26.12 and 31.48 hours.