Answer:
No of real solutions =1
No of extraneous solution =2
Real solution: x =3
Explanation:
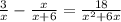
solving:
Taking LCM of x, x+6 and x^2+6 we get x(x+6)
Multiply the equation with LCM
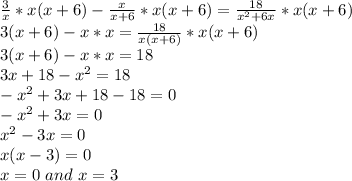
Checking for extraneous solution
for extraneous solution we check the points where the solution is undefined
The solution will be undefined. if, x=0 or x=-6 so both are extraneous solutions
Putting x =3

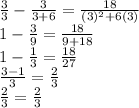
So, x=3 is real solution.
Now, Selecting answers from tables
No of real solutions =1
No of extraneous solution =2
Real solution: x =3