Answer:
These set of lengths cannot be the side lengths of a right angled triangle.
Explanation:
Pythagoras Theorem is always followed by a right angled triangle. According to which the sum of squares of the two shorter legs is equal to the square of the longest leg.
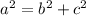
So here, 17 is the longest leg and 7 and 12 the shorter ones.
Applying Pythagoras Theorem to these lengths to find out.
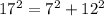
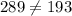
Therefore, these set of lengths cannot be the side lengths of a right angled triangle.