Question

Proof true or false: For all integers a,b,and c,if ab|c then a|c and b|c

Answer 1

Answer with explanation:

It is given that for three integers , a, b and c, if

`(ab)/(c)\rightarrow then, (a)/(c) \text{or} (b)/(c)`

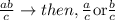
Since , a b is divisible by c , following are the possibilities

1.→ a and b are prime integers .Then , c will be prime number either equal to a or b.

2.→a and b are not prime integers ,then any of the factors of a or b will be equal to c.For example:

⇒a=m × n

b=p × q× c

or,

⇒a=u×v×c

b=s×t

So, whatever the integral values taken by a, and b, if
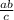`(ab)/(c)` then either of
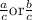`(a)/(c) \text{or} (b)/(c)` is true.