Question

Find the coordinates of point B that lies along the directed line segment from A(-5, 2) to C(11, 0) and partitions the segment in the ratio of 5:3.

A. (3, 1)
B. (5,3/4)
C. (10, 5)
D. (6, 2)

Answer 1

B. (5,3/4)

Explanation:

Since, when a segment having end points
`(x_1, y_1)` and
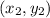`(x_2, y_2)` is divided by or partitioned by a point, that lies on the segment, in the ratio of m : n,

Then the coordinates of that points are,

`((mx_2+nx_1)/(m+n), (my_2+my_1)/(m+n))`

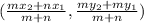
Here, point B that lies along the directed line segment from A(-5, 2) to C(11, 0) and partitions the segment in the ratio of 5:3,

Thus, the coordinates of B are,

`((5* 11+3* -5)/(5+3), (5* 0+3* 2)/(5+3))`

`((55-15)/(8), (0+6)/(8))`

`((40)/(8), (6)/(8))`

`(5, (3)/(4))`

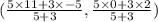
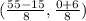
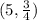
Option 'B' is correct.

Answer 2

The correct answer is B.

EXPLANATION

If the point B(x,y) partitions

`A(x_1,y_1)`

and

`C(x_2,y_2)`

in the ratio m:n then, then we have

`x = (mx_2+nx_1)/(m + n)`

and

`y= (my_2+ny_1)/(m + n)`

We want to find the coordinates of the point B(x,y) that lies along the directed line segment from A(-5, 2) to C(11, 0) and partitions the segment in the ratio of 5:3.

This implies that:

`x = (5 * 11+3 * - 5)/(5 + 3)`

`\implies \: x = (55 - 15)/(8)`

`\implies \: x = (40)/(8) = 5`

`y = (5 * 0 + 3 * 2)/(5 + 3)`

`y = (0 + 6)/(8)`

`y = (6)/(8) = (3)/(4)`

Therefore the coordinates of B are

`(5, (3)/(4) )`