Answer: x=1; y=-5
Step-by-step explanation: To solve this system we can use differente methods, in this case we are going to use substitution:
first equation: 3x+10y=-47
second equation: 5x-7y=40
we are going to isolate x from the first equation:
3x=-47-10y

now we replace it in the second equation:
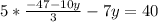
and now we solve for y:
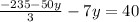
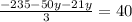
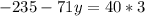
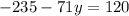
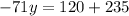
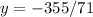
y=-5
now we replace the value of y in the first equation and solve for x:

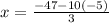
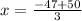
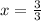
x=1