Answer:
Either
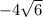 or
or
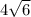 , depending on whether
, depending on whether
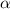 is larger than
is larger than
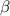 .
.
Explanation:
The two roots (might necessarily be distinct or real) of the quadratic equation
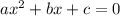 , where
, where
 ,
,
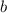 , and
, and
 are constants and
are constants and
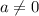 are
are
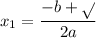 , and
, and
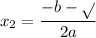 .
.
The difference between the two will be either:
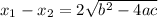 or
or
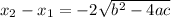 .
.
For this question,
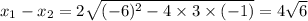 , or
, or
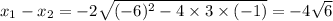 .
.