Question

Two simple pendulums are in two different places. The length of the second pendulum is 0.4 times the length of the first pendulum, and the acceleration of gravity experienced by the second pendulum is 0.9 times the acceleration of gravity experienced by the first pendulum. Determine the comparison of the frequency of the first pendulum to the second pendulum. a) 2/3. b) 3/2 (5 marks) c) 4/9. d) 9/4

Answer 1

`\sqrt{(4)/(9)}`

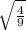
Step-by-step explanation:

The frequency of a simple pendulum is given by:

`f=(1)/(2\pi)\sqrt{(g)/(L)}`

where

g is the acceleration of gravity

L is the length of the pendulum

Calling
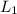`L_1` the length of the first pendulum and
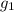`g_1` the acceleration of gravity at the location of the first pendulum, the frequency of the first pendulum is

`f_1=(1)/(2\pi)\sqrt{(g_1)/(L_1)}`

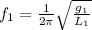
The length of the second pendulum is 0.4 times the length of the first pendulum, so

`L_2 = 0.4 L_1`

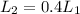
while the acceleration of gravity experienced by the second pendulum is 0.9 times the acceleration of gravity experienced by the first pendulum, so

`g_2 = 0.9 g_1`

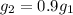
So the frequency of the second pendulum is

`f_2=(1)/(2\pi)\sqrt{(g_2)/(L_2)}=(1)/(2\pi) \sqrt{(0.9 g_1)/(0.4 L_1)}`

Therefore the ratio between the two frequencies is

`(f_1)/(f_2)=\frac{(1)/(2\pi)\sqrt{(g_1)/(L_1)}}{(1)/(2\pi) \sqrt{(0.9 g_1)/(0.4 L_1)}}=\sqrt{(0.4)/(0.9)}=\sqrt{(4)/(9)}`