Answer:
The similar triangles are Δ KMJ and Δ NML
The value of x is 3
KM = 6 and NM = 3
Explanation:
* Lets revise the cases of similarity
1) AAA similarity : two triangles are similar if all three angles in the first
triangle equal the corresponding angle in the second triangle
- Example : In ΔABC and ΔDEF, m∠A = m∠D, m∠B = m∠E and
m∠C= m∠F then ΔABC ≈ ΔDEF by AAA
2) AA similarity : If two angles of one triangle are equal to the
corresponding angles of the other triangle, then the two triangles
are similar.
- Example : In ΔPQR and ΔDEF, m∠P = m∠D, m∠R = m∠F then
ΔPQR ≈ ΔDEF by AA
3) SSS similarity : If the corresponding sides of two triangles are
proportional, then the two triangles are similar.
- Example : In ΔXYZ and ΔLMN, if
then the two triangles are similar by SSS
4) SAS similarity : In two triangles, if two sets of corresponding sides
are proportional and the included angles are equal then the two
triangles are similar.
- Example : In triangle ABC and DEF, if m∠A = m∠D and
then the two triangles are similar by SAS
* Now lets solve the problem
- ∠KMJ is a aright angle and M is on JL
∴ m∠JML = 180° ⇒ straight angle
∵ m∠JMK + m∠LMN = m∠JML
∴ 90° + m∠NML = 180° ⇒ subtract 90° from both sides
∴ m∠NML = 90°
- In Δ KMJ and ΔNML
∵ m∠KMJ = m∠NML ⇒ proved
∵ m∠KJM = m∠NLM ⇒ given
- By using the second case above (AA similarity)
∴ Δ KMJ ≈ Δ NML
* The similar triangles are Δ KMJ and Δ NML
- From similarity
∴ Their sides are proportion
∴
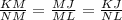
∵ KJ = 10 and NL = 5
∵ KM = 3 + x and NM = x
- Substitute these values in the proportion relation
∵

∴
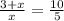
- By using cross multiplication
∴ 5(3 + x) = 10(x) ⇒ simplify
∴ 5(3) + 5(x) = 10x
∴ 15 + 5x = 10x ⇒ subtract 5x from both sides
∴ 15 = 5x ⇒ divide both sides by 5
∴ 3 = x
* The value of x is 3
∵ KM = 3 + x
∵ x = 3
∴ KM = 3 + 3 = 6
∵ NM = x
∴ NM = 3
* KM = 6 and NM = 3
- Check the ratio
∵ KM/NM = 6/3 = 2
∵ KJ/NL = 10/5 = 2
∴ The sides are proportion