Question

A 15 in. windshield wiper makes a 150° arc across the windshield.

About how far does the end of the windshield wiper travel?

Answer 1

`\displaystyle (25)/(2)\pi \approx 39.3` inches.

Explanation:

The question gives the central angle and radius of an arc and is asking for the length.

• The radius is the same as the length of the windshield wiper: 15 inches.
• The central angle is 150°.

An arc is part of a circle. What is the circumference of a circle with a radius 15 inches?

`\text{Circumference} = \pi * \text{Diameter} = 2\pi * \text{Radius} = 30\pi` inches.

However, this wiper traveled only a fraction of the circle. A full circle is
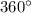`360^(\circ)`. The central angle of this arc is only
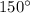`150^(\circ)`. As a result,

`\displaystyle \frac{\text{Length of this arc}}{\text{Circumference of the circle}} = (150^(\circ))/(360^(\circ)) = (5)/(12)`.

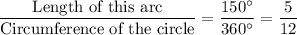The length of the arc will thus be

`\displaystyle (5)/(12) * 30\pi = (25)/(2)\pi \approx 39.3`.

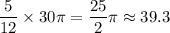In other words, the windshield wiper traveled approximately 39.3 inches.