Question

Craig is standing on his apartment balcony and locates his car in the street-level parking lot below. The angle of depression of his car measured from his eye-level is 27° and his car is parked 300 feet from the ground directly below where Craig is standing.

How high is the base of Craig's balcony from the ground to the nearest foot, if Craig's eye-level is 6 feet from the base of the balcony?
A. 583 feet
B. 147 feet
C. 261 feet
D. 130 feet

Answer 1

B. 147 feet

Explanation:

We can easily imagine a right triangle for this problem. The height of the triangle is what we're looking for (x), at the bottom of x, we have the right angle formed by the building and the ground. The other side of that right angle is the distance to the car (300 ft). On top of the x side, we have the angle of 63 degrees looking down, since Craig is looking down by 27 degrees (90 - 27 = 63).

We can easily apply the Law of Sines that says:

`(a)/(sin(A)) = (c)/(sin(C))`

Then we can isolate c and fill in the values:

`c = (a * sin(C))/(sin(A)) =(300 * sin(27))/(sin(63)) = 153`

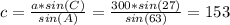
So, we know Craig's eyes are 153 feet above ground... since Craig is 6 feet tall, the balcony sits at 147 feet high (153 - 6 = 147).