Question

The point slope form of the equation of the line that passes through (-5-1) and (10.-7) is

standard form of the equation for this line?

Answer 1

The standard form of the equation for this line can be:

l: 2x + 5y = -15.

Explanation:

Start by finding the slope of this line.

For a line that goes through the two points
`(x_0, y_0)` and
`(x_1, y_1)`,

`\displaystyle \text{Slope} = (y_(1) - y_(0))/(x_(1) - x_(0))`.

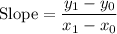For this line,

`\displaystyle \text{Slope} = ((-1) - (-7))/((-5) - 10) = -(2)/(5)`.

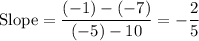Find the slope-point form of this line's equation using

• 
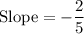  `\displaystyle \text{Slope} = -(2)/(5)`, and
• The point
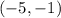  `(-5, -1)` (using the point
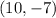  `(10, -7)` should also work.)

The slope-point form of the equation of a line

• with slope
  `m` and
• point
  `(x_(0), y_(0))`

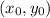
should be
`l:\; y - y_(0) = m(x - x_0)`.

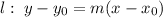For this line,

• 
  `\displaystyle m = -(2)/(5)`, and
• 
  `x_0 = -5`, and
• 
  `y_0 = -1`.

The equation in slope-point form will be

`\displaystyle l:\; y - (-1) = -(2)/(5)(x - (-5))`.

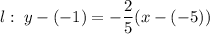The standard form of the equation of a line in a cartesian plane is

`l: \; ax + by = c`

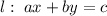
where

`a`,
`b`, and
`c` are integers.
`a \ge 0`.

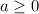Multiply both sides of the slope-point form equation of this line by
`5`:

`l:\; 5 y + 5 = -2x -10`.

Add
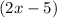`(2x-5)` to both sides of the equation:

`l: \; 2x + 5y = -15`.

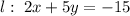Therefore, the equation of this line in standard form is
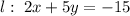`l: \; 2x + 5y = -15`.