Hello!
The answer is:
The correct option is:
A.
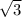
Why?
Since we already know the hypothenuse and the opposite side of the triangle (y), we can calculate the value of "x" using the Pythagorean Theorem.
We have that:
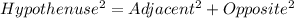
We know that:
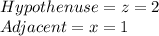
So, substituting and calculating we have:
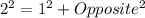
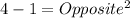
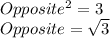
Then,using the following trigonometric relation:
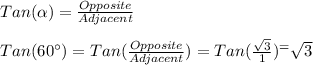
We have that the correct option is:
A.
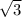
Have a nice day!