Answer:
$12,993.71
Explanation:
The formula we want for this is exponential decay which is
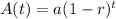
where A(t) is the value of the car after the depreciation, a is the initial value of the car, r is the interest rate at which it depreciates in decimal form, and t is the time in years. We have everything we need to fill in to solve for A(t):
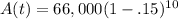
We will do some simplifying first:
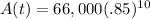
First raise .85 to the 10th power to get
A(t) = 66,000(.1968744043)
and then multiply to get
A(t) = $12,993.71