Question

A camper wants to know the width of a river. From point A, he walks downstream 60 feet to point B and sights a canoe across the river. It is determined that
`\alpha` = 34°. About how wide is the river?

A. 34 feet
B. 50 feet
C. 89 feet
D. 40 feet

Answer 1

Answer: OPTION D

Step-by-tep explanation:

Observe the figure attached.

You can notice that the the width of the river is represented with "x".

To calculate it you need to use this identity:

`tan\alpha=(opposite)/(adjacent)`

In this case:

`\alpha=34\°\\opposite=x\\adjacent=60`

Now you must substitute values:

`tan(34\°)=(x)/(60)`

And solve for "x":

`60*tan(34\°)=x\\\\x=40.4ft`

`x`≈
`40ft`

Answer 2

Hello!

The answer is:

The correct option is:

D. 40 feet.

Why?

To solve the problem and calculate the width of the river, we need to assume that the distance from A to B and the angle formed between that distance and the distance from A to the other point (C) is equal to 90°, meaning that we are working with a right triangle, also, we need to use the given angle which is equal to 34°. So, to solve the problem we can use the following trigonometric relation:

`Tan\alpha =(Opposite)/(Adjacent)`

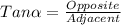
Where,

alpha is the given angle, 34°

Adjacent is the distance from A to B, which is equal to 60 feet.

Opposite is the distance from A to C which is also equal to the width of the river.

So, substituting and calculating we have:

`Tan(34\°) =(Width)/(60ft)`

`Width=60ft*Tan(34\°)=60ft*0.67=40.2ft=40ft`

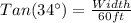
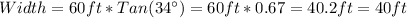
Hence, we have that the correct option is:

D. 40 feet.

Have a nice day!