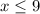Answer:
- The derivative of the function is:
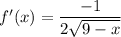
- The domain of the function is:
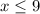
- and the domain of the derivative function is:
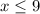
Explanation:
The function f(x) is given by:
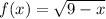
The domain of the function is the possible values of x where the function is defined.
We know that the square root function
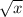 is defined when x≥0.
is defined when x≥0.
Hence,
 will be defined when
will be defined when
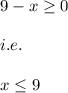
Hence, the domain of the function f(x) is:
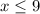
Also, the definition of derivative of x is given by:
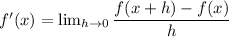
Hence, here by putting the value of the function we get:
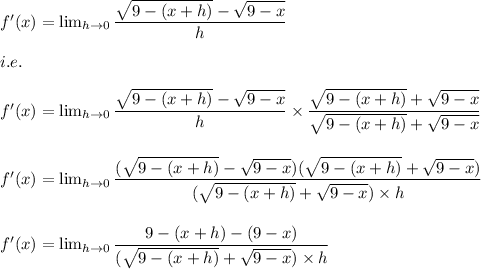
Since,
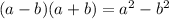
Hence, we have:
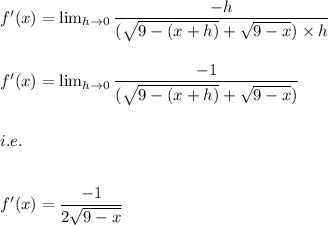
Since, the domain of the derivative function is equal to the derivative of the square root function.
Also, the domain of the square root function is:
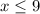
Hence, domain of the derivative function is: