Question

Doug drew two identical triangles. He wants to prove the converse of the Pythagorean Theorem by using both triangles. The first triangle has side lengths of 12 cm, 16 cm, and 20 cm, such that 122 + 162 = 202. Using the converse of the Pythagorean Theorem, enter the length of the side opposite the 90° angle of the second triangle.______cm

Answer 1

Doug can use two identical triangles to prove the converse of the Pythagorean Theorem. The length of the side opposite the 90° angle in the second triangle is 20 cm.

Step-by-step explanation:

To prove the converse of the Pythagorean Theorem, Doug can use two identical triangles. In the first triangle, with side lengths of 12 cm, 16 cm, and 20 cm, he already found that 12² + 16² = 20². Now, since the triangles are identical, the side lengths of the second triangle are also 12 cm, 16 cm, and 20 cm. Using the converse of the Pythagorean Theorem, the length of the side opposite the 90° angle in the second triangle is 20 cm.

Answer 2

Answer is explained in the explanation section

Step-by-step explanation:

Solution:

Converse of the pythagorean theorem helps us to check whether a triangle is a right triangle or not. Converse of the pythagorean theorem is simply the opposite of the pythagoren theorem. Pythagorean theorem states that, if triangle is right triangle, then
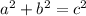`a^(2) + b^(2) = c^(2)`. On the other hand, Converse of the Pythagorean theorem states that, if
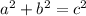`a^(2) + b^(2) = c^(2)`, then triangle is a right triangle.

Pythagorean theorem =
`c^(2) = a^(2) + b^(2)`

Converse of the pythagorean theorem =
`a^(2) + b^(2) ? c^(2)`

First of all let's check the first triangle is right triangle or not.

a = 12

b= 16

c= 20

So,

`a^(2) + b^(2) = c^(2)`.

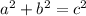144 + 256 = 400

400 = 400

Yes, 1st triangle is no doubt a right triangle. On the other hand, we are given that 2nd triangle = right triangle as we are given the 90 degree angle already. Here, we know that triangle is a right triangle

hence,
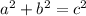`a^(2) + b^(2) = c^(2)`. will surely be there.

Now, we have find out the side opposite to the 90 degrees angle, which is c.

we also know that, right triangles sides follow the pattern of 3x,4x and 5x

Since, c is the longest side.

Hence, c= 5x