Question

A child is sliding on a sled at 1.5 m/s to the right. You stop the sled by pushing on it for 0.60 s in a direction opposite to its motion. If the mass of the child and sled is 41 kg, what is the magnitude of the average force you need to apply to stop the sled? Use the concepts of impulse and momentum. Express your answer with the appropriate units.

Answer 1

102.5 N

Step-by-step explanation:

The impulse theorem applied to this situation states that:

`F \Delta t = m \Delta v`

where

F is the average force applied on the child and the sled

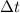`\Delta t` is the time interval during which the force is applied

The term on the right represents the variation of momentum, which is the product of:

m is the mass of the child+sled

`\Delta v` is the change in velocity of the child+sled

In this situation we have:

`\Delta v = 0 - 1.5 m/s = -1.5 m/s`

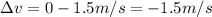
m = 41 kg

`\Delta t = 0.60 s`

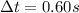
So we can solve to find the average force:

`F=(m\Delta v)/(\Delta t)=((41 kg)(-1.5 m/s))/(0.60 s)=-102.5 N`

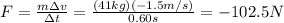
And the negative sign means the force is applied against the direction of motion of the child. So the magnitude of the force is 102.5 N.