Answer:
C
Explanation:
If there is an expression such as:
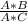
we can cancel out A from top and bottom and that will leave us with
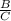
Note: Let A, B, C, be any algebraic expression
For the problem given, we can simply cut (x+1) from top and bottom by rules of algebra. So the remaining terms are:
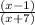
This is option C