Question

On a test, mean score was 70 and the standard deviation of the scores was 15.

What is the probability that a randomly selected test taker scored below 50?

Answer 1

`P(x\:<\:50)=0.0918`

Explanation:

To find the probability that a randomly selected test taker scored below 50, we need to first of all determine the z-score of 50.

The z-score for a normal distribution is given by:

`z=(x-\bar x)/(\sigma)`.

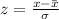From the question, the mean score is
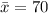`\bar x=70`, the standard deviation is,
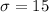`\sigma=15`, and the test score is
`x=50`.

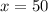We substitute these values into the formula to get:

`z=(50-70)/(15)`.

`z=(-20)/(15)=-1.33`.

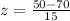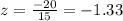We now read the area that corresponds to a z-score of -1.33 from the standard normal distribution table.

From the table, a z-score of -1.33 corresponds to and area of 0.09176.

Therefore the probability that a randomly selected test taker scored below 50 is
`P(x\:<\:50)=0.0918`