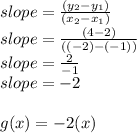Answer:
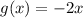
Explanation:
A point reflected across the y-axis maintains its y-coordinate, but its x-coordinate switches signs. So, a positive x-coordinate becomes negative, and a negative x-coordinate becomes positive.
Let's take a few points from the original function, f(x). Remember, if we know the function, we can find the y-coordinate for any x-coordiante by simply plugging it into the function's equation.
Generally,

So:
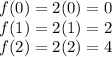
Leading us to have the plot points (0,0), (1,2) and (2,4).
To reflect this across the y-axis for the g(x) equation, we just need to turn the x-coordinates negative, resulting in a set of (0,0), (-1,2), and (-2,4).
Since we know this is a linear function (because there are no exponents in the equation), we can calculate the slope of this new set of points by using just 2 of them. The slope will give us our equation, because since (0,0) is a point on our line, we know that the y-intercept is zero.