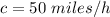Answer:
The maximum speed of Hal's airplane in still air is:
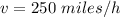
The speed of the wind
Explanation:
Remember that the velocity v equals the distance d between time t.
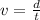 and
and

The distance that Hal travels when traveling with the wind is:
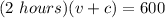 miles
miles
Where v is the speed of Hal and c is the wind speed.
The distance when traveling against the wind is:
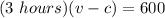 miles
miles
Now we solve the first equation for v
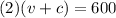
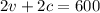
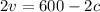
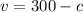
Now we substitute the value of v in the second equation and solve for c
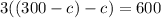

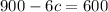

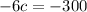

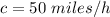
Then:
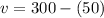
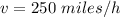
The maximum speed of Hal's airplane in still air is:
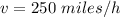
The speed of the wind