Question

When doing blood testing for a viral infection, the procedure can be made more efficient and less expensive by combining partial samples of different blood specimens. If samples from three people are combined and the mixture tests negative, we know that all three individual samples are negative. Find the probability of a positive result for three samples combined into one mixture, assuming the probability of an individual blood sample testing positive for the virus is 0.03.

Answer 1

The best way to approach this type of problem is to use the "complement method" ...

P(positive result) = 1 - P(negative result)

= 1 - (1 - 0.03)^3

= 1 - 0.97^3 = 0.087327 or 8.7%

Step-by-step explanation:

Answer 2

`0.087`

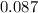
Step-by-step explanation:

Given -

Probability of positive blood sample for an individual is equal to 0.03

Number of sample is equal to three

Now , probability of getting a positive result for three sample combined into one single mixture is equal to

`1 - (P)^ 3`

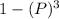
where P represents the probability of getting all individual negative test result

Substituting the given values in above equation, we get

`P_(mixture) = 1 - (1-0.03)^3\\P_(mixture) = 1- (0.97)^3\\P_(mixture) = 0.087`