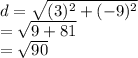Answer:
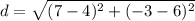
Explanation:
The expression used for calculating distance between two points involves the square root of sum of squares of differences of x-intercepts and y-intercepts.
The formula is given by:
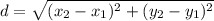
Here,
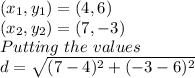
Hence, the following expression will give the distance between given points
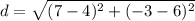
Solving it will give: