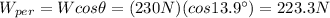Question

a 230-newton box rests on a plank 5 meters long. One end is 1.2 meters higher than the other end. Find the components of the force the box exerts

Answer 1

55.3 N, 223.3 N

Step-by-step explanation:

First of all, we can find the angle of the inclined plane.

We have:

L = 5 m the length of the incline

h = 1.2 m is the height

We also have the relationship

`h = L sin \theta`

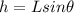
where
`\theta` is the angle of the incline. Solving for the angle,

`\theta= sin^(-1) ((h)/(L))=sin^(-1) ((1.2 m)/(5 m))=13.9^(\circ)`

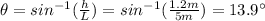
Now we can find the components of the weight of the box, which is the force that the box exerts on the plank. Calling W = 230 N the weight of the box, we have:

- Component parallel to the incline:

`W_(par) = W sin \theta = (230 N)(sin 13.9^(\circ)) =55.3 N`

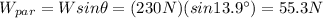
- Component perpendicular to the incline:

`W_(per) = W cos \theta = (230 N)(cos 13.9^(\circ)) =223.3 N`